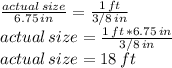Question

Architects create drawings to model the buildings that will eventually get built. These drawings are

done in a program called CAD and are always created to scale. One particular drawing is created with a
scale of 3/8 in = 1ft.
a. If a certain wall is 8 feet tall, write a proportion to solve for the inches this wall would
represent on an architectural drawing.
b. Solve the proportion in part (a).
c. The length of a room is drawn as 6.75 inches. Write a proportion to solve the actual length in
feet of the room.
d. Solve the proportion in part (c).

Answer 1

a)
`(8 \,ft)/(reduced\,drawing) =(1\,ft)/(3/8\,in)`

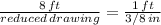
b) Reduced drawing size = 3 in

c)
`(actual\,size)/(6.75\,in) =(1\,ft)/(3/8\,in)`

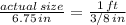
d) actual length of the room: 18 ft

Explanation:

The proportion that CAD creates is given by:

`(actual\,size)/(reduced\,drawing) =(1\,ft)/(3/8\,in)`

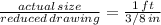
Then:

a) if a wall is 8 ft tall, the proportion gives:

`(actual\,size)/(reduced\,drawing) =(1\,ft)/(3/8\,in)\\(8\,ft)/(reduced\,drawing) =(1\,ft)/(3/8\,in)`

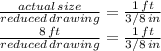
b) to solve this proportion for the reduced drawing size, we cross multiply and then isolate the unknown on one side by dividing both sides by "1 ft":

`(8\,ft)/(reduced\,drawing) =(1\,ft)/(3/8\,in)\\3/8\, in \,*\,8\,ft=reduced\,drawing\,*\,1\,ft\\reduced\,drawing=(3/8\,in\,*\,8\,ft)/(1\,ft)\\reduced\,drawing=3 \,in`

c) If the drawing shows a room with length 6.75 in, we use the proportion equation again, replacing now the "reduced drawing" quantity with 6.75 in, and getting ready to solve for the unknown "actual size":

`(actual\,size)/(reduced\,drawing) =(1\,ft)/(3/8\,in)\\(actual\,size)/(6.75\,in) =(1\,ft)/(3/8\,in)`

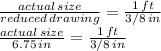
d) To solve for the unknown, since it is already in the numerator, we just need to multiply both sides of the equal sign by 6.75 in:

`(actual\,size)/(6.75\,in) =(1\,ft)/(3/8\,in)\\actual\,size= (1\,ft\,*6.75\,in)/(3/8\,in) \\actual\,size=18\,ft`