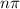Answer:
The function touches the damping factor
at x=
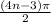 and x=
and x=

The x-intercept of f(x) is
at x=
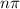
Explanation:
Given function is f(x)=
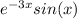 and damping factor as y=
and damping factor as y=
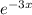 and y=
and y=
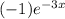
To find when function touches the damping factor:
For f(x)=
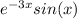 and y=
and y=
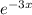
Equating the both the equation,

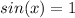
x=
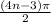
For f(x)=
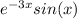 and y=
and y=
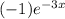
Equating the both the equation,

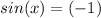
x=

Therefore, The function touches the damping factor x=
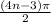 and x=
and x=

To find x-intercept of f(x):
For x-intercept, y=0
f(x)=
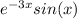
y=
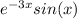
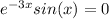
Hence,
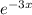 is always greater than zero.
is always greater than zero.
Therefore,

x=
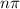
Thus,
The x-intercept of f(x) is at x=