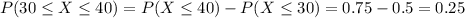Answer:
a) 0.37
b) 0.421
c) 0.25
Explanation:
Since the probability of winning a game is binomial (P = 0.5) the expected value for number of winning when you play 60 games is
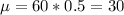
And the standard deviation:
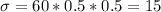
a) the cumulative probability of winning at least 35 games is
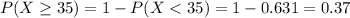
b)
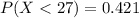
c)