Question

You consider yourself a bit of an expert at playing rock-paper-scissors and estimate that the probability that you win any given game is 0.5. In a tournament that consists of playing 60 games of rock-paper-scissors let X be the random variable that is the of number games won. Assume that the probability of winning a game is independent of the results of previous games. You should use the normal approximation to the binomial to calculate the following probabilities. Give your answers as decimals to 4 decimal places. a)Find the probability that you win at least 35 of the games. P(X ≥ 35) =b)Find the probability that you win less than 27 games. P(X < 27) =c)Find the probability that you win between 30 and 40 games. P(30 ≤ X ≤ 40) =

Answer 1

a) 0.37

b) 0.421

c) 0.25

Explanation:

Since the probability of winning a game is binomial (P = 0.5) the expected value for number of winning when you play 60 games is

`\mu = 60*0.5 = 30`

And the standard deviation:

`\sigma = 60*0.5*0.5 = 15`

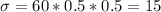
a) the cumulative probability of winning at least 35 games is

`P(X \geq 35) = 1 - P(X < 35) = 1 - 0.631 = 0.37`

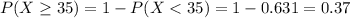
b)
`P(X < 27) = 0.421`

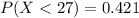
c)
`P(30 \leq X \leq 40) = P(X \leq 40) - P(X \leq 30) = 0.75 - 0.5 = 0.25`