Answer:
y = 6x - 1
Explanation:

(0, -1) ⇒ x₁ = 0, y₁ = -1
(1, 5) ⇒ x₂ = 1, y₂ = 5
So the slope:
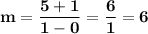
The slope-intercept form of the equation of line is y = mx + b, where m is the slope and b is the y-intercept of the line.
(0, -1) ⇒ x₀ = 0, y₀ = -1 ⇒ b = -1
Therefore:
y = 6x - 1 ← the slope-intercept form of the equation