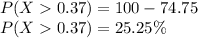Question

4. The diameters of bolts produced by a certain machine are normally distributed with a mean of 0.35 inches and a standard deviation of 0.03 inches. What percentage of bolts will have a diameter greater than 0.37 inches? Round your answer to two decimal places.

Answer 1

25.25%

Step-by-step explanation:

Mean diameter (μ) = 0.35 inches

Standard deviation (σ) = 0.03 inches

For any given diameter, X, the z-score is given by:

`z=(X-\mu)/(\sigma)`

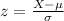
For X= 0.37 inches:

`z=(0.37-0.35)/(0.03)\\z=0.6667`

A z-score of 0.6667 is equivalent to the 74.75-th percentile of a normal distribution.

Therefore, the percentage of bolts that will have a diameter greater than 0.37 inches is:

`P(X>0.37) = 100 - 74.75\\P(X>0.37) = 25.25\%`