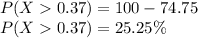Answer:
25.25%
Step-by-step explanation:
Mean diameter (μ) = 0.35 inches
Standard deviation (σ) = 0.03 inches
For any given diameter, X, the z-score is given by:
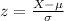
For X= 0.37 inches:
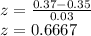
A z-score of 0.6667 is equivalent to the 74.75-th percentile of a normal distribution.
Therefore, the percentage of bolts that will have a diameter greater than 0.37 inches is: