Question

One positive integer is 3 greater than 4 times another positive integer. If the product of the two integers is 76, then what is the sum of the two integers?

14
23
21
19

Answer 1

The sum of the two integers is 23

Explanation:

Let one integer be x and the other integer be y

Then according to the statement "One positive integer is 3 greater than 4 times another positive integer.."

x be the integer that is One positive integer is 3 greater than 4 times another positive integer.

Then

x= 3+4y----------------------------------(1)

Product of the two integer is 76, this can written as

`x * y =76`

substituting the values of x from eq(1)

`( 3+4y) * y =76`

`3y + 4y^2 = 76`

`3y + 4y^2-76= 0`

`4y^2 + 3y -76= 0`

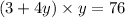
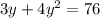
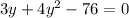
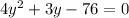
Solving the quadratic equation equation we get

`x=(-b \pm √(b^2-4ac))/(2a)`

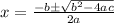
here

a = 4

b= 3

c = -76

susbtituting the above values in the formula

`y=(-3 \pm √(3^2-4(4)(-76)))/(2(4))`

`y=(-3 \pm √(9- 4(4)(-76)))/(8)`

`y=(-3 \pm √(9- (16)(-76)))/(8)`

`y=(-3 \pm √(9- (-1216)))/(8)`

`y=(-3 \pm √(9 + 1216))/(8)`

`y=(-3 \pm √(1225))/(8)`

`y=(-3 \pm 35)/(8)`

`y=(-3 +35)/(8)`
`y=(-3 -35)/(8)`

`y=(32)/(8)`
`y=(-38)/(8)`

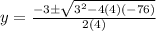
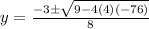
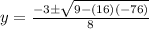
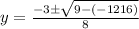
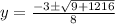
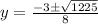
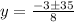
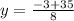
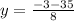
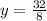
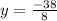
y= 4 y = −4.75

Since in the question it is given that it is a positive integer

so y = 4

substituting y=4 in eq (1) we get,

x= 3+4(4)

x= 3+16

x= 19

The sum of the two integers

=> x + y

=> 19+4

=>23