Answer:
The sum of the two integers is 23
Explanation:
Let one integer be x and the other integer be y
Then according to the statement "One positive integer is 3 greater than 4 times another positive integer.."
x be the integer that is One positive integer is 3 greater than 4 times another positive integer.
Then
x= 3+4y----------------------------------(1)
Product of the two integer is 76, this can written as
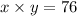
substituting the values of x from eq(1)
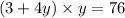
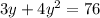
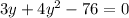
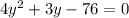
Solving the quadratic equation equation we get
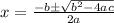
here
a = 4
b= 3
c = -76
susbtituting the above values in the formula
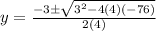
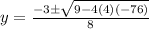
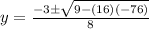
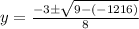
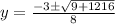
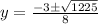
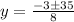
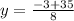
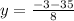
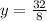
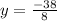
y= 4 y = −4.75
Since in the question it is given that it is a positive integer
so y = 4
substituting y=4 in eq (1) we get,
x= 3+4(4)
x= 3+16
x= 19
The sum of the two integers
=> x + y
=> 19+4
=>23