Answer:
![r_(cm)=[12.73,12.73]cm](https://img.qammunity.org/2020/formulas/physics/high-school/rjfm34apw0vjdl49je2u4i83ub1463t7cu.png)
Step-by-step explanation:
The general equation to calculate the center of mass is:
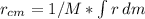
Any differential of mass can be calculated as:
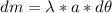 Where "a" is the radius of the circle and λ is the linear density of the wire.
Where "a" is the radius of the circle and λ is the linear density of the wire.
The linear density is given by:

So, the differential of mass is:

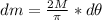
Now we proceed to calculate X and Y coordinates of the center of mass separately:
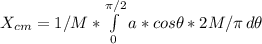
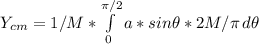
Solving both integrals, we get:
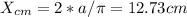

Therefore, the position of the center of mass is:
![r_(cm)=[12.73,12.73]cm](https://img.qammunity.org/2020/formulas/physics/high-school/rjfm34apw0vjdl49je2u4i83ub1463t7cu.png)