Question

A uniform thin wire is bent into a quarter-circle of radius a = 20.0 cm, and placed in the first quadrant. Determine the coordinates of its center of mass with respect to the origin of coordinates at the center of the "full" circle.

Answer 1

`r_(cm)=[12.73,12.73]cm`

Step-by-step explanation:

The general equation to calculate the center of mass is:

`r_(cm)=1/M*\int\limits {r} \, dm`

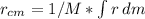
Any differential of mass can be calculated as:

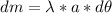`dm = \lambda*a*d\theta` Where "a" is the radius of the circle and λ is the linear density of the wire.

The linear density is given by:

`\lambda=M/L=M/(a*\pi/2)=(2M)/(a\pi)`

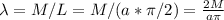
So, the differential of mass is:

`dm = (2M)/(a\pi)*a*d\theta`

`dm = (2M)/(\pi)*d\theta`

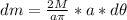
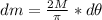
Now we proceed to calculate X and Y coordinates of the center of mass separately:

`X_(cm)=1/M*\int\limits^(\pi/2)_0 {a*cos\theta*2M/\pi} \, d\theta`

`Y_(cm)=1/M*\int\limits^(\pi/2)_0 {a*sin\theta*2M/\pi} \, d\theta`

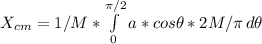
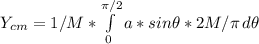
Solving both integrals, we get:

`X_(cm)=2*a/\pi=12.73cm`

`Y_(cm)=2*a/\pi=12.73cm`

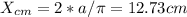
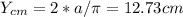
Therefore, the position of the center of mass is:

`r_(cm)=[12.73,12.73]cm`