Question

the area of a rectangle is 108 in^2 . if the length is 12 inches longer then the width, find the dimensions of the rectangle

Answer 1

The length and width of rectangle are 18 inches and 6 inches respectively

Solution:

Given that area of rectangle is 108 square inches

Let "L" be the length of rectangle

Let "W" be the width of rectangle

To find: dimenions of rectangle. i.e length and width

Given that length is 12 inches longer then the width

Length = 12 + width

L = 12 + W

The area of rectangle is given as:

`\text {Area of rectangle }=\text { length } * \text { width }`

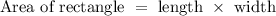
Substituting the given values in above formula,

`\begin{array}{l}{108=L * W} \\\\ {108=(12+W) * W} \\\\ {108=12 W+W^(2)} \\\\ {W^(2)+12 W-108=0}\end{array}`

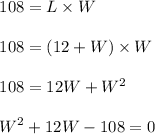
Let us solve the above quadratic equation using quadratic formula

`\text {For a quadratic equation } a x^(2)+b x+c=0`

`x = \frac{-b \pm \sqrt{\left(b^(2)-4 a c\right)}}{2 a}`

`\text {So for } \mathrm{W}^(2)+12 \mathrm{W}-108=0, \text { we get } \mathrm{a}=1 \text { and } \mathrm{b}=12 \text { and } \mathrm{c}=-108`

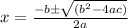
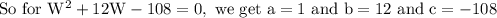
Substituting the values in quadratic formula,

`\begin{aligned} W &=\frac{-12 \pm \sqrt{12^(2)-4(1)(-108)}}{2 * 1} \\\\ W &=(-12 \pm √(144+432))/(2) \\\\ W &=(-12 \pm √(576))/(2)=(-12 \pm 24)/(2) \\\\ W &=(-12+24)/(2) \text { or } W=(-12-24)/(2) \\\\ W &=6 \text { or } W=-18 \end{aligned}`

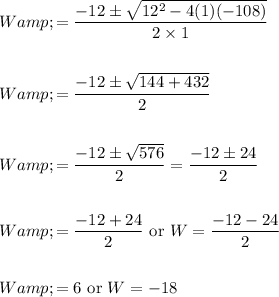
Since width cannot be negative, ignore negative value

So width of rectangle = 6 inches

L = 12 + W = 12 + 6 = 18 inches

So the length and width of rectangle are 18 inches and 6 inches respectively