The length and width of rectangle are 18 inches and 6 inches respectively
Solution:
Given that area of rectangle is 108 square inches
Let "L" be the length of rectangle
Let "W" be the width of rectangle
To find: dimenions of rectangle. i.e length and width
Given that length is 12 inches longer then the width
Length = 12 + width
L = 12 + W
The area of rectangle is given as:
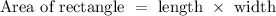
Substituting the given values in above formula,
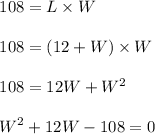
Let us solve the above quadratic equation using quadratic formula
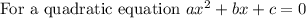
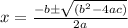
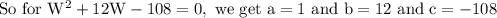
Substituting the values in quadratic formula,
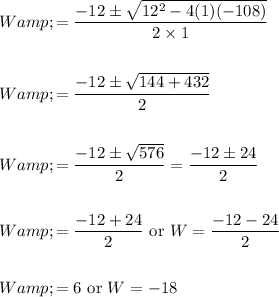
Since width cannot be negative, ignore negative value
So width of rectangle = 6 inches
L = 12 + W = 12 + 6 = 18 inches
So the length and width of rectangle are 18 inches and 6 inches respectively