Answer:
The mass of the ball is 0.23 kg
Step-by-step explanation:
Given that
radius ,r= 3.74 cm
Density of the milk ,ρ = 1.04 g/cm³ = 1.04 x 10⁻³ kg/cm³
Normal force ,N= 9.03 x 10⁻² N
The volume of the ball V

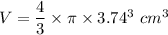
V= 219.13 cm³
The bouncy force on the ball = Fb
Fb = ρ V g
Fb + N = m g
m=Mass of the ball = Density x volume
m = γ V , γ =Density of the Ball
ρ V g + N = γ V g ( take g= 10 m/s²)
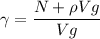
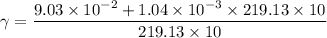
γ = 0.00108 kg/cm³
m = γ V
m = 0.00108 x 219.13
m= 0.23 kg
The mass of the ball is 0.23 kg