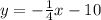Answer:
B.
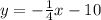
Explanation:
Given rectangle with sides J,K,L and M.
We need to find equation of sides that are perpendicular to side K.
For a rectangle adjacent sides are perpendicular to each other.
For side K, the adjacent sides are J and L. Hence, sides J and L are perpendicular to side L.
Finding equation of side J.
Points: (-5,4) and (3,2)
Slope of line

where
 and
and
 are points on the line.
are points on the line.
Thus
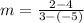
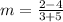
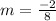
Simplifying fraction.
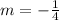
Using point-slope equation to find equation of the line.
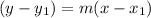
Using point (-5,4)

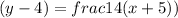
Using distribution
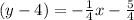
Adding 4 to both sides.
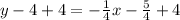
Taking LCD to add fraction.
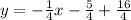
Equation of side J.
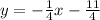
Finding equation of side L.
Points: (-8,-8) and (0,-10)
Slope of line

where
 and
and
 are points on the line.
are points on the line.
Thus

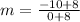
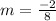
Simplifying fraction.
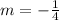
Using point-slope equation to find equation of the line.
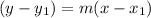
Using point (0,-10)

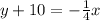
Subtracting both sides by 10.
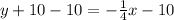
Equation of side L.
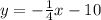
The equation of side perpendicular to side K is represented by