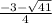Answer:
The Roots of f(x) are
x=1
x=
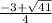
and x=
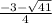
Explanation:
Given function f(x)=
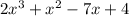
We know that
A. The sum of coefficient of polynomial is zero then, (x-1) is one of root of polynomial
f(1)=0
B. The difference of sum of coefficient of odd term and sum of coefficient of even term of polynomial is zero then, (x+1) is one of root of polynomial
f(-1)=0
Let x=1
f(1)=
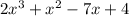
f(1)=2+1-7+4=0
Therefore, (x-1) is one of root.
Let x=(-1)
f(1)=
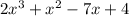
f(1)=-2+1+7+4=10
Therefore, (x-1) is not one of root.
Using Remainder theorem:
Dividing (x-1) on both the side.
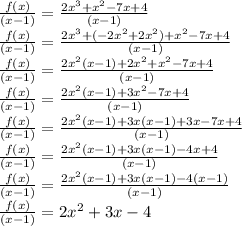
For 2x^{2}+3x-4
a=2,b=3 and c=(-4)
D=

D=
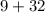
D=
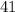
x=
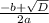 and x=
and x=
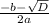
x=
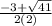 and x=
and x=
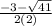
x=
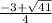 and x=
and x=
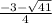
Thus,
The Roots of f(x) are
x=1
x=
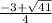
and x=