Question

Chevy has some yarn that he wants to use to make hats and scarves. Each hat uses 0.20.20, point, 2 kilograms of yarn and each scarf uses 0.10.10, point, 1 kilograms of yarn. Chevy wants to use 222 kilograms of yarn to make a total of 151515 items. Let hhh be the number of hats Chevy makes and sss be the number of scarves he makes. Which system of equations represents this situation? Choose 1 answer:

Answer 1

`0.2h+0.1s=2\\h+s=15`

Explanation:

This is based off the way khan said it was right when I had this problem

Answer 2

The system of equation that represent this situations are;

`\left \{ {{h+s=15} \atop {0.2h+0.1s=2}} \right.`

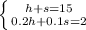
Also 5 hats and 10 scarves can be prepared from 2 kg of yarn.

Explanation:

Let number of hat Chevy makes be h.

Also Let number of scarves Chevy makes be s.

Given:

Total Amount of yarns = 2 kg

Total number of items = 15

Since Items need to make are hat and scarves.

Hence the equation can be represented as;

`h+s=15 \ \ \ \ equation \ 1`

Again Given:

Each hat uses 0.2 kilograms of yarn.

each scarf uses 0.1 kilograms of yarn.

Hence the equation can be represented as;

`0.2h+0.1s=2 \ \ \ \ \ equation \ 2`

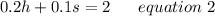
Hence the system of equation that represent this situations are;

`\left \{ {{h+s=15} \atop {0.2h+0.1s=2}} \right.`

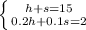
Now Solving these to find number of hats and number of scarves.

Multiplying equation 2 with 10 we get;

`10(0.2h+0.1s)=2* 10\\10*0.2h+10*0.1s=20\\2h+s =20 \ \ \ \ \ equation \ 3`

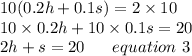
Now Subtracting equation 1 from equation 3 we get;

`(2h+s)- (h+s) =20-15\\2h+s-h-s=5\\h= 5`

Now Substituting the value of h in equation 1 we get;

`h+s= 15\\5+s =15\\s=15-5\\s=10`

Hence 5 hats and 10 scarves can be prepared from 2 kg of yarn.