Answer:
The resulting power density is enough to melt the metal.
Explanation:
Given data:
Power = P = 3000 J/sec
diameter = d = 3.5 mm
Solution:
As we Know that Area = A = π r² ---- (1)
where r is radius.
Also Radius =
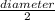
Putting the values of radius, π = 3.14 in equation 1, we get
A = 3.14 x (
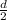 )²
)²
A = 3.14 x (3.5/2)²
A = 9.62 mm²
As 75% of heat is concentrated in circular area then Power P becomes
P = 3000 J/sec x 75 %
As J/sec = Watt = W and 75 % = 3/4
so P = 3000 W x 3/4
P = 2250 W
As power density is represented by the formula:
Power density = PD = P/A
where P is Power and A is area.
So,
PD = P/A
Putting the values of Power and Area in above equation, we get
PD = 2250 W / 9.62 mm²
PD = 234 W/mm²
So, this power density is sufficient to melt the metal.