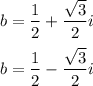Answer:
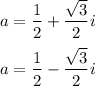
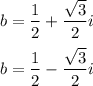
Explanation:
Recall that
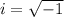
so

we have then
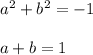
Isolating b in the second equation we get
b = 1-a
Replace this value in the first equation
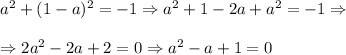
Solving the quadratic equation we get two possible solutions for a
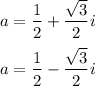
Replacing these values in b=1-a, we get two possible solutions for b