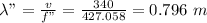Question

A stationary bagpiper is playing a Highland bagpipe, in which one reed produces a continuous sound of frequency 440 Hz. The air is still and the speed of sound is 340 m/s. A) What is the wavelength of the sound wave produced by the bagpipe?B)What is the frequency of the sound wave that a bicyclist hears if she is approaching the bagpiper at 10.0 m/s?C)What is the wavelength of the sound wave that a bicyclist hears if she is approaching the bagpiper at 10.0 m/s?D)What is the frequency of the sound wave that a bicyclist hears if she is moving away from the bagpiper at 10.0 m/s?E)What is the wavelength of the sound wave that a bicyclist hears if she is moving away from the bagpiper at 10.0 m/s?

Answer 1

(A) 0.773 m

(B) f' = 452.94 Hz

(C)
`\lambda' = 0.751\ m`

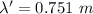
(D) f" = 427.058 Hz

(E)
`\lambda' = 0.796\ m`

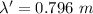
Solution:

As per the question:

Frequency of the sound produced, f = 440 Hz

Speed of the sound in still air, v = 340 m/s

Now,

(A) To calculate the wavelength of the sound wave:

We use the relation:

`v = f\lambda`

`\lambda = (340)/(440) = 0.773\ m`

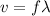
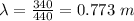
(B) By using Doppler effect to calculate the frequency of the sound wave:

Velocity of the receiver,
`v_(R) = 10.0\ m/s`

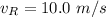
Velocity of the source,
`v_(S) = 0\ m/s`

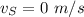
When the receiver is approaching:

`f' = (v + v_(R))/(v)f = (340 + 10)/(340)* 440`

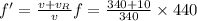
f' = 452.94 Hz

(C) To calculate the wavelength of the sound wave:

`\lambda' = (v)/(f') = (340)/(452.94) = 0.751\ m`

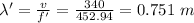
(D) While moving away, the frequency of the sound wave can be calculated as:

`f`

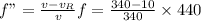
f" = 427.058 Hz

(E) The wavelength can be given by:

`\lambda`