Question

Please help me with both of these questions I’m supper stuck

Answer 1

ONE SOLUTION

Explanation:

When two points on a line are given, the equation of the line is given by the formula:

`$ (y - y_1)/(y_2 - y_1) = (x - x_1)/(x_2 - x_1) $`

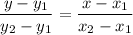
where
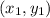`$ (x_1, y_1) $` and
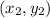`$ (x_2, y_2) $` are the points on the line.

Here, the first set of points are:
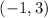`$ (-1, 3) $` and
`$ (0, 1) $`.

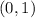Therefore,
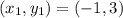`$ (x_1, y_1) = (-1, 3) $` and
`$ (x_2,y_2) = (0, 1) $`.

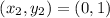The line passing through this is given by:

`$ (y - 3)/(1 - 3) = (x + 1)/(1) $`

`$ \implies y - 3 = -2x - 2 $`

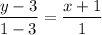
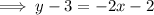
∴ 2x + y - 1 =0

Now, for the second line, the points are:

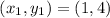`$ (x_1, y_1) = (1, 4) $` and
`$ (x_2, y_2) = (0, 2) $`.

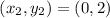Therefore,
`$ (y - 4)/(-2) = (x - 1)/(-1) $`

`$ \implies -y + 4 = -2x + 2 $`

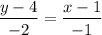
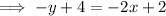
∴ 2x - y + 2 = 0

Now, to determine the number of solutions the two equations have, we solve these two equations,

Adding Eqn(1) and Eqn(2) we get:

4x = -1

`$ \implies x = (-1)/(4) $`

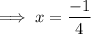
And
`$ y = (3)/(2) $`.

Since, we arrive at unique values of 'x' and 'y', we say the lines have only one unique solution.