To solve this problem we must simply resort to Newton's second law as well as the relationship between pressure and force as a physical unit applied in a given area.
In mathematical terms the Weight can be expressed as
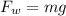
Where,
m = mass
g = Gravitational Acceleration
We have the mass and the gravitational acceleration therefore the Weight is
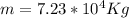
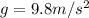
Replacing we have
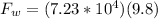
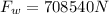
In this way the pressure exerted according to the active Area is,
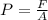
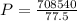
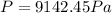
Therefore the pressure difference between the lower and upper surface of the wings is 9.14kPa