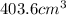Answer : The correct option is, (C)
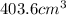
Explanation :
The formula used for the volume expansion coefficient is:
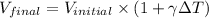
where,
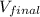 = final volume of mercury = ?
= final volume of mercury = ?
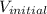 = initial volume of mercury =
= initial volume of mercury =
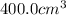
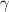 = volume expansion coefficient =
= volume expansion coefficient =
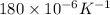
 = change in temperature =
= change in temperature =
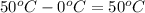
Now put all the given values in the above formula, we get:
![V_(final)=400.0* [1+(180* 10^(-6)* 50)]](https://img.qammunity.org/2020/formulas/chemistry/college/1l1zdt85bq2o4rdf2yf7r8e0ovfmripdpw.png)
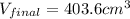
Therefore, the final volume of mercury is