Question

A certain sample of a gas has a volume of 20.00 dm3 at 0 °C and 1.000 atm. A plot of the experimental data of its volume against the Celsius temperature, θ, at constant p, gives a straight line of slope 0.0741 dm3 °C−1. From these data alone (without making use of the perfect gas law), determine the absolute zero of temperature in degrees Celsius.

Answer 1

`\theta_o = (20 dm^3)/(0.0741 C^(-1))=269.91 C`

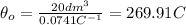
Explanation:

Notation

`V_i` represent the intercept for the linear model

`\theta` represent the temperature in Celsius degrees

`V` represent the volume for a given temperature on dm^3

For this case we have a linear model relating the volume V, with the temperature
`\theta` and with constant pressure.

So for this case the linear model would be:

`V= 0.0741 \theta + V_i`

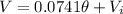
We have an initial condition given
`\theta=0 C, V= 20dm^3`

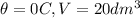
If we use this condition in the linear model we can find the intercept:

`20=0.0741*0+V_i`

So for this case the intercept is
`V_i =20`

So th linear model is given by:

`V=0.0741 \theta +20`

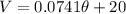
We are interedtes on the absolute zero temperature, and that occurs when the volume V=0, and assuming this we can find the temperature
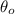`\theta_o` where we have the absolute zero temperature. So we can set up the equation like this:

`0=0.0741 \theta_o +20`

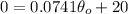
And solving for
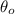`\theta_o` we got:

`\theta_o = (20 dm^3)/(0.0741 C^(-1))=269.91 C`

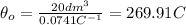
And that's our final answer.