Answer:
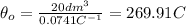
Explanation:
Notation
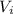 represent the intercept for the linear model
represent the intercept for the linear model
 represent the temperature in Celsius degrees
represent the temperature in Celsius degrees
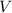 represent the volume for a given temperature on dm^3
represent the volume for a given temperature on dm^3
For this case we have a linear model relating the volume V, with the temperature
 and with constant pressure.
and with constant pressure.
So for this case the linear model would be:
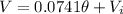
We have an initial condition given
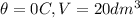
If we use this condition in the linear model we can find the intercept:
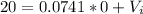
So for this case the intercept is
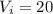
So th linear model is given by:
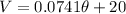
We are interedtes on the absolute zero temperature, and that occurs when the volume V=0, and assuming this we can find the temperature
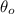 where we have the absolute zero temperature. So we can set up the equation like this:
where we have the absolute zero temperature. So we can set up the equation like this:
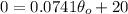
And solving for
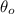 we got:
we got:
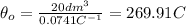
And that's our final answer.