Question

A spring stretched by 8.0 cm has an energy of 20.J. The same spring is stretched by 12 cm. What is the elastic potential energy in the spring at this elongation

Answer 1

To solve this problem we need to use the equations related to Elastic Potential Energy, which allows us to know the Energy stored in a spring based on its elastic constant and its respective compression. By definition it is described as

`PE = (1)/(2)kx^2`

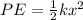
Where,

k = Spring constant

x = Displacement

Our values are given as

`x_1= 0.08m`

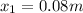
As we do not know the spring constant but if the energy stored at the compression given then,

`PE = (1)/(2)kx^2`

`20 = (1)/(2)k(0.08)^2`

`k = 6250N/m`

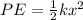
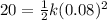
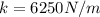
In the case of the second compression and understanding that the spring constant is intrinsic to the internal force of the spring, then

`x_2 = 0.12m`

Replacing,

`PE = (1)/(2)(6250)(0.12)^2`

`PE = 45J`

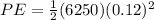
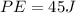
Therefore the elastic potential energy in the spring at this elongation is 45J