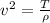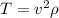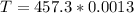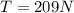To solve this problem it is necessary to apply the concepts related to string vibration. A vibration in a string is a wave. Resonance causes a vibrating string to produce a sound with constant frequency, i.e. constant pitch,
The speed of propagation of the wave in a string is proportional to the square root of the tension and inversely proportional to the root of the linear density. Mathematically this can be expressed as

At the same time we have that the frequency is subject to the wavelength and the speed. That is to say
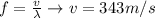 Speed of sound at 20°C.
Speed of sound at 20°C.
Therefore the frequency would be
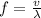
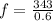

While that is the auditory frequency, the frequency caused in the string would be
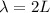
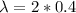
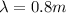
So reusing the frequency formula we can find that now the velocity in the string is of
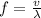

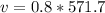
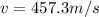
Finally using the vibration in the string we can find the tension, so: