Find the vertical asymptote(s) of f of x equals quantity 2 x squared plus 3x plus 6 end quantity over quantity x squared minus 1. x = −1, 1 x = 1, 2 x = −1, 2 x = −2, 2

Question

asked Sep 4, 2020 33.6k views

2 Answers

Mythofechelon · Answer 1 · 2020-09-11T19:05:10+0000

Answer:

x = −1, 1

Explanation:

Vertical Asymptotes

A vertical asymptote of the graph of a given function f(x) is the line x=a, such that one of of these statements is fulfilled

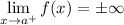
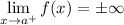
$\displaystyle \lim _(x\to a^(+))f(x)=\pm \infty$

If f(x) is a rational expression, we must find all the values of x who make the denominator equal to zero

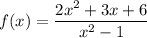
$\displaystyle f(x)=(2x^2+3x+6)/(x^2-1)$

We set the denominator to zero

x^2-1=0

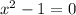
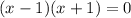
(x-1)(x+1)=0

$x=-1,\ x=1$

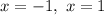
Those are the vertical asymptotes of f