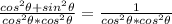Question

Consider the Pythagorean Identity cos 2 ( θ ) + sin 2 ( θ ) = 1 cos2⁡(θ)+sin2⁡(θ)=1. Divide both sides of this identity by cos 2 ( θ ) cos2⁡(θ) and simplify the resulting equation. What is the result?

Answer 1

Therefore we have another identity:

`(cos^(2)\theta +sin^(2)\theta)/(cos^(2)\theta*cos^(2)\theta)=(1)/(cos^(2)\theta*cos^(2)\theta)`

`(1)/(cos^(2)\theta*cos^(2)\theta)=(1)/(cos^(2)\theta*cos^(2)\theta)`

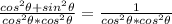
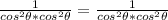
Explanation:

1) Considering the Pythagorean, or the Fundamental Trigonometric Identity Identity:

`cos^(2)\theta +sin^(2)\theta =1`

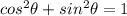
2)Let's divide both sides, the left and the right one by:

`cos^(2)\theta*cos^(2)\theta`

3) Since
`cos^(2)\theta +sin^(2)\theta` is equal to 1, then we can replace it. So

`cos^(2)\theta +sin^(2)\theta =1\Rightarrow (cos^(2)\theta +sin^(2)\theta)/(cos^(2)\theta*cos^(2)\theta)=(1)/(cos^(2)\theta*cos^(2)\theta)\Rightarrow (1)/(cos^(2)\theta*cos^(2)\theta)=(1)/(cos^(2)\theta*cos^(2)\theta)`

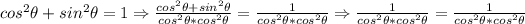
Therefore we have another identity:

`(cos^(2)\theta +sin^(2)\theta)/(cos^(2)\theta*cos^(2)\theta)=(1)/(cos^(2)\theta*cos^(2)\theta)`