Answer:
2.64 mm
Step-by-step explanation:
We are given that
Distance between two slits=0.310=
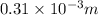
1 mm=
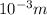
Distance between slit and screen=4.3 m
Wavelength of red light =
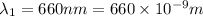
1 nm=
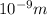
Wavelength of blue light=
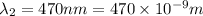
We have to find the distance on the screen between the first order bright fringe for each wavelength.
We know that
The distance between the first order bright fringes on the screen is given by
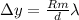
Where
R=Distance between screen and slits
m=Order of fringe=1
d=distance between two slits
 Difference in wavelength of two light source
Difference in wavelength of two light source
Substitute the values then we get
Distance between the first order bright fringes on the screen for two sources =
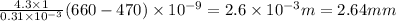
Hence, the distance between the first order bright fringes on the screen for two light sources=2.64mm