Question

Coherent light that contains two wavelengths, 660 nm (red) and 470 nm (blue), passes through two narrow slits that are separated by 0.310 mm. Their interference pattern is observed on a screen 4.30 m from the slits. What is the disatnce on the screen between the first order bright fringe for each wavelength?

Answer 1

2.64 mm

Step-by-step explanation:

We are given that

Distance between two slits=0.310=
`0.31* 10^(-3) m`

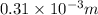
1 mm=
`10^(-3) m`

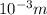
Distance between slit and screen=4.3 m

Wavelength of red light =
`\lambda_1=660 nm=660* 10^(-9) m`

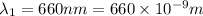
1 nm=
`10^(-9)m`

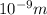
Wavelength of blue light=
`\lambda_2=470 nm=470* 10^(-9) m`

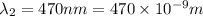
We have to find the distance on the screen between the first order bright fringe for each wavelength.

We know that

The distance between the first order bright fringes on the screen is given by

`\Delta y=(Rm)/(d)\Delat \lambda`

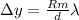
Where

R=Distance between screen and slits

m=Order of fringe=1

d=distance between two slits

`\Delta \lambda=` Difference in wavelength of two light source

Substitute the values then we get

Distance between the first order bright fringes on the screen for two sources =
`(4.3* 1)/(0.31* 10^(-3))(660-470)* 10^(-9)=2.6 * 10^(-3) m=2.64 mm`

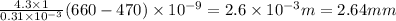
Hence, the distance between the first order bright fringes on the screen for two light sources=2.64mm