Question

A cylinder with rotational inertia I l = 2.0 kg . m2 rotates clockwise about a vertical axis through its center withangular speed ml = 5.0 rad] S. = 5.0 rad/s. A second cylinderwith rotational inertia [2 = 1.0 kg . m2rotates counter clockwise about the same axis with angular speed m2 = 8,0 rad/s , If the cylinders couple so theyhave the same rotational axis what is the angular speed of the combination? What percentage of the original kineticenergy is lost to friction?

Answer 1

`W_s = 0.67 rad/s`

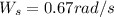
it is lost the 98.82% of the energy.

Step-by-step explanation:

for answer this, we will use the conservation of the angular momentum L:

`L_f = L_i`

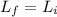
so:

`I_1W_1 + I_2W_2 = I_sW_s`

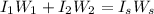
where
`I_1` is the moment of inertia,
`W_1` is the angular velocity of the cylinder 1,
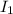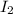`I_2` is the moment of inertia of the second cylinder,
`W_2` is the angular velocity of the second cylinder,
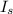`I_s` is the moment of inertia of the cylinders couple and
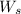`W_s` is the angular velocity of the cylinders couple

note: we will take the clockwise rotation as positive.

Replacing the values, we get:

`(2 kg*m^2)(5 rad/s) + (1 kg*m^2)(-8 rad/s) = (3 kg*m^2)W_s`

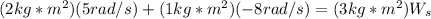
solving for
`W_s`:

`W_s = 0.67 rad/s`

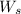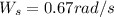
for find the kinetic energy lost we must calculate the initial Ei and the final energy Ef as:

`E_i = (1)/(2)I_1W_1^2+(1)/(2)I_2W_2^2`

`E_i = (1)/(2)(2)(5)^2+(1)/(2)(1)(8)^2`

`E_i = 57 J`

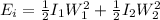
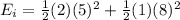
and,

`E_f = (1)/(2)I_sW_s^2`

`E_f = (1)/(2)(3)(0.67)^2`

`E_f = 0.67335 J`

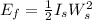
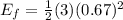
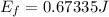
now, the percentage of the original kinetic energy that is lost to friction is calculated as:

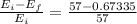`(E_i-E_f)/(E_i)=(57-0.67335)/(57)` = 0.9882 = 98.82%

that means that was lost the 98.82% of the energy.