Rate at which area is increasing is 1.08 m²/s.
Explanation:
Area of triangle is with side a and b and angle C between them is given by
A = 0.5 ab SinC
Here we need to find how area changes with a and b fixed and C is changing,
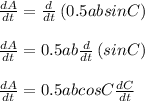
We have
a = 8 m
b = 9 m
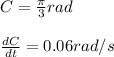
Substituting

Rate at which area is increasing is 1.08 m²/s.