Answer:
Given
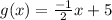 we can conclude the following things:
we can conclude the following things:
A)
 is one-to-one.
is one-to-one.
B)
 's inverse is given by
's inverse is given by
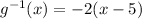 .
.
Explanation:
A) If it is one-to-one, then f(a)=f(b) implies only a=b.
The function is
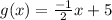 .
.
Let's see what
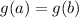 implies here.
implies here.
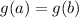
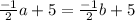
Subtract 5 on both sides:

Multiply both sides by -2:
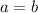
This is exactly what we need to show that
 is one-to-one.
is one-to-one.
---------------------------------------------------------------------------------------------
If you look at a visual of
 on a graph. You would see it passes the horizontal line test making it one-to-one. (It is is just a diagonal line after all.)
on a graph. You would see it passes the horizontal line test making it one-to-one. (It is is just a diagonal line after all.)
B)
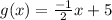

The inverse is the swapping of
 and
and
 and then we want to remake the new
and then we want to remake the new
 the subject of the equation.
the subject of the equation.
That is we have to solve the following for
 :
:
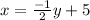
Subtract 5 on both sides:
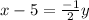
Multiply both sides by -2:
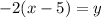
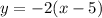
So
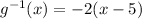 .
.
--------------------------------------------------------------------------------------------
Let's verify.
So we should get that
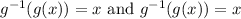 .
.
Let's see what happens:
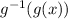


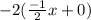
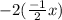
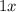
 -So that looks good so far.
-So that looks good so far.
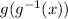
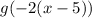
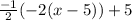
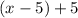
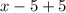
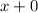
 -So that looks good.
-So that looks good.
Both ways check out so we indeed found the inverse of
 .
.