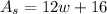Answer:
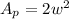
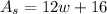
Explanation:
Functions and Geometry
Sometimes we need to express areas, volumes, and distances in terms of unknown quantities (or variables). When we can find such expressions, they can be referred to as functions. Let's recall the area of a rectangle is A=wl, being w its wide and l its length
Please refer to the image below. The length of the swimming pool is l and its width is w. Its area is
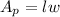
We know the length is twice as long as its width, l=2w, so
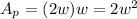
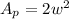
The sidewalk is 2 feet wide. The length of the pool and its sidewalk is
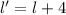
Similarly, the width of the pool+sidewalk is
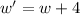
The area of the pool+sidewalk is
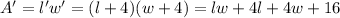
We know that l=2w, so
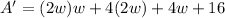
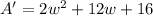
The area of the sidewalk alone is the subtraction of both areas
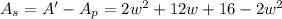
Simplifying