Question

On a coordinate plane, a solid straight line has a positive slope and goes through (0, negative 1.3) and (3, negative 0.3). Everything below and to the right of the line is shaded.

Which linear inequality is represented by the graph?

y ≤ One-thirdx – 1.3
y ≤ One-thirdx – Four-thirds
y ≥ One-thirdx – Four-thirds
y ≥ One-thirdx – 1.3

Answer 1

A

Explanation:

`slope=(-0.3-(-1.3))/(3-0)=(1)/(3)\\eq.~of~line~is y-(-1.3)=(1)/(3)(x-0)\\y=(1)/(3)x-1.3\\as~it~is~shaded~to~the~right~so~y\leq (1)/(3)x-1.3~satisfies ~it.`

Answer 2

A.
`y\leq (1)/(3)x-1.3`.

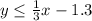Explanation:

We have been given that or a coordinate plane, a solid straight line has a positive slope and goes through
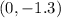`(0, -1.3)` and
`(3, -0.3)`. Everything below and to the right of the line is shaded. We are asked to choose the inequality that represents the graph.

First of all, we will find the slope of line using our given points as:

`m=(-0.3-(-1.3))/(3-0)`

`m=(-0.3+1.3)/(3)`

`m=(1)/(3)`

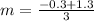
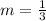
Now we will use point-slope form of equation to find the equation of boundary line as:

`y-y_1=m(x-x_1)`

`y-(-1.3)=(1)/(3)(x-0)`

`y+1.3=(1)/(3)x`

`y+1.3-1.3=(1)/(3)x-1.3`

`y=(1)/(3)x-1.3`

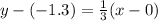
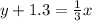
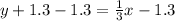
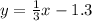
The one side of line would be
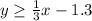`y\geq (1)/(3)x-1.3` and other side of the boundary line would be
`y\leq (1)/(3)x-1.3`.

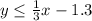Now we will graph our line.

We can see that the point (0,6) is on right side of boundary line, so we will test (0,6) in both inequalities.

`6\leq (1)/(3)(0)-1.3`

`6\leq 0-1.3`

`6\leq -1.3`

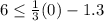
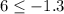
Since point (0,6) satisfies the inequality
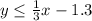`y\leq (1)/(3)x-1.3`, therefore, our required inequality would be
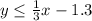`y\leq (1)/(3)x-1.3` and option A is the correct choice.