Answer:
A.
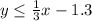 .
.
Explanation:
We have been given that or a coordinate plane, a solid straight line has a positive slope and goes through
 and
and
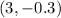 . Everything below and to the right of the line is shaded. We are asked to choose the inequality that represents the graph.
. Everything below and to the right of the line is shaded. We are asked to choose the inequality that represents the graph.
First of all, we will find the slope of line using our given points as:
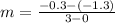
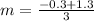
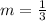
Now we will use point-slope form of equation to find the equation of boundary line as:
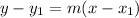
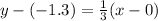
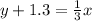
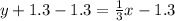
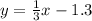
The one side of line would be
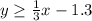 and other side of the boundary line would be
and other side of the boundary line would be
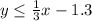 .
.
Now we will graph our line.
We can see that the point (0,6) is on right side of boundary line, so we will test (0,6) in both inequalities.
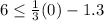
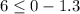
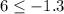
Since point (0,6) satisfies the inequality
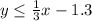 , therefore, our required inequality would be
, therefore, our required inequality would be
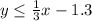 and option A is the correct choice.
and option A is the correct choice.