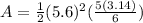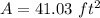Question

What is the area of a sector with a central angle of tradians and a radius of 5.6 ft?

Use 3.14 for it and round your final answer to the nearest hundredth.
Enter your answer as a decimal in the box.

Answer 1

`A=41.03\ ft^2`

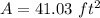
Explanation:

The complete question is

What is the area of a sector with a central angle of 5π/6 radians and a radius of 5.6 ft? Use 3.14 for π and round your final answer to the nearest hundredth.

we know that

The area of a sector is given by the formula:

`A=(1)/(2)r^2\theta`

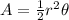
where

A is the area,

r is the radius

`\theta` is the angle in radians.

we have

`r=5.6\ ft`

`\theta=(5\pi)/(6)`

`\pi =3.14`

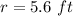
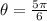
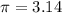
substitute the values

`A=(1)/(2)(5.6)^2((5(3.14))/(6))`

`A=41.03\ ft^2`