Question

The top and bottom margins of a poster are 6 ft and the side margins are each 8 ft. If the area of printed material on the poster is fixed at 386 square ft, find the dimensions of the poster with the smallest area.

Answer 1

Dimension

Height =29.01

Breadth=38.70

Explanation:

Printed area is =386 and margins as specified.

For printed area let height be x and breadth be y.

x*y=386 ⇒ y =
`(386)/(x)`

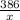
Now considering the margins

Height = x+6+6=x+12

Weidth =
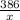`(386)/(x)` +8 +8=
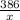`(386)/(x)` + 16

Area of poster to be minimised =(x+12)(
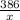`(386)/(x)` + 16)

Differentiate above area with respect to x and equate to zero to find extrema.

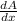`(dA)/(dx)` = 16 -
`(12*386)/(x^(2) )`=0

x=17.01

Now plug value of x in height and breadth

Height =29.01

Breadth=38.70