Answer:
After 10 hours, both tanks would have the same amount of water.
Explanation:
The first tank has 130 gallons already, that's its initial condition, and it's being filled by 10 gallons every hour. This can be modeled by the following equation

Where
 represents hours.
represents hours.
The second tank has 280 gallons of water, that's its initial condition, and it's being drained by 5 gallons every hour. In this case, "drained" refers to a negative variation
 .
.
Now, we need to make them equal, because we need to find how many hours will take to have the same amount of water. So,
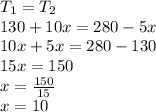
Therefore, after 10 hours, both tanks would have the same amount of water.