Answer: 1.424 N
Step-by-step explanation:
According to Newton's Universal Law of Gravitation:
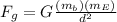 (1)
(1)
Where:
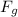 is the gravitational force between the ball and Earth
is the gravitational force between the ball and Earth
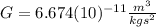 the Universal Gravitational Constant
the Universal Gravitational Constant
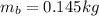 is the mass of the ball
is the mass of the ball
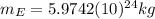 is the mass of the Earth
is the mass of the Earth
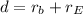 is the distance between the ball and the Earth, being
is the distance between the ball and the Earth, being
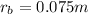 the radius of the ball and
the radius of the ball and
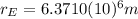 the radius of the Earth
the radius of the Earth
So, rewritting (1):
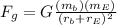 (2)
(2)
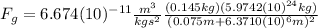 (3)
(3)
Finally:
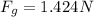 (4)
(4)