Answer:
The ratio is 2:1
Step-by-step explanation:
The relation between activation energy, temperature and reaction constant is formulated as Arrhenius equation, which is:
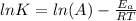
Where
K = rate constant
A= frequency factor
T= temperature (K)
R= gas constant
Here A and R both are constant for the two given conditions
So
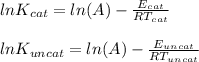
Equating the two
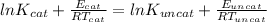
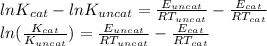
)/(K_(uncat))=2](https://img.qammunity.org/2020/formulas/chemistry/high-school/rjisfjyz1nnuad0vi5vs2h9ddg7hjn1sph.png) )=\frac{14000}{8.314X362}-\frac{11900}{8.314X362}=0.698[/tex]
)=\frac{14000}{8.314X362}-\frac{11900}{8.314X362}=0.698[/tex]
Taking antilog