Question

A 50 (ohm) lossless transmission line is terminated in a load with impedance Z= (30-j50) ohm. the wavelength is 8cm. Determine:

(a) reflection coefficient (solved: 0.1 - j0.56 or 0.56 angle -79.9)
(b) standing wave ratio (solved: 3.64)
(c) position of voltage max. nearest the load
(d) position of current max. nearest the load

Answer 1

Reflection Coefficient =
`0.57e^(-i79.8)`

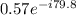
SWR=3.65

Position of
`V_(max) =3.11cm`

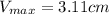
position of
`i_(max) =1.11cm`

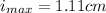
Step-by-step explanation:

To determine the above answers, let outline the useful formulas

refection coefficient
`p=(terminalimpednce -characteristics impedance )/(terminalimpednce +characteristics impedance ) \\`.

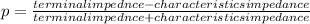where terminal impednce = (30-i50)Ω

characteristics impedance= 50Ω

Secondly, the Standing Wave Ratio,
`SWR=(1+/p/)/(1-/p/)`

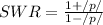
Now let us substitute values and solve,

a.
`p=(terminalimpednce -characteristics impedance )/(terminalimpednce +characteristics impedance ) \\`

`p=((30-i50)-50)/((30-i50)-50) \\`

`p=(-20-i50)/(80-i50) \\`

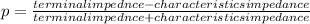
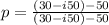
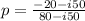
multiplying the numerator and denominator by the conjugate of the denominator. we have

`p=(-20-i50)/(80-i50)*(80+i50)/(80+i50)\\`

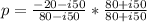
by carrying out careful operation, we arrived at

`p=(900-i5000)/(8900) \\p=0.1011-i0.56179\\`

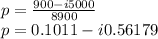
To express in polar form i.e
`re^(i alpha)`

`r=\sqrt{0.1011^(2)+0.56179^(2)} \\r=0.57\\`

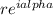
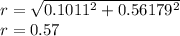
to get the angle

alpha=
`tan^(-1) (0.56179)/(0.1011) \\alpha=-79.8\\`

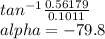
hence the Reflection Coefficient,p =
`0.57e^(-i79.8)`

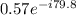
b. we now determine the Standing Wave Ratio,
`SWR=(1+/p/)/(1-/p/)`

`swr=(1+0.57)/(1-0.57) =3.65\\`

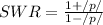
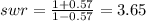
c. to determine the position of the maximum voltage nearest to the load,

we use the equation

`Position of V_(max)=(\alpha λ)/(4\pi)+(λ)/(2)\\`

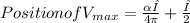
were
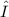`λ` is the wavelength of 8cm

lets convert α to rad by multiplying by π/180

`Position of V_(max)=(-79.8 *8cm*\pi)/(4\pi*180 ) +(8cm)/(2) \\`

`Position of V_(max)=-0.89+4.0=3.11cm\\`.

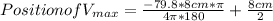
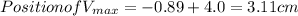d. also were we have minimum voltage,there the maximum current will exist, to find this position nearest to the load

`Position of v_(min)=Position of V_(max)-(λ)/(4) \\\\Position of v_(min)=3.11cm-(8cm)/(4)=1.11cm`.

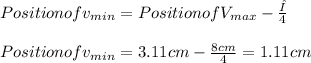since the voltage minimum occure at 1.11cm. we can conclude that the current maximum also occur at this point i.e 1.11cm