Answer:
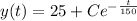
Explanation:
We are given that differential equation

We have to find the expression for the temperature of the coffee at time t.
Let y be the temperature of the coffee in degree C and t be the time in minutes.
At t=0 , y=85 degree Celsius
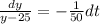
Integrating on both sides

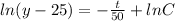
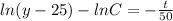
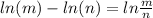
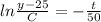
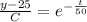

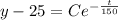
Substitute the value t=0 and y=85 then we get
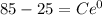
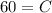
Substitute the value of C
Then , we get
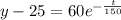
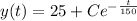
This is required expression for the temperature of the coffee at time t.