Question

The differential equation below models the temperature of a 85 degree C cup of coffee in a 25 degree C room, where it is know that the coffee cools at a rate 1 degree C per minute when its temperature is 75 degree C. Solve the differential equation to find an expression for the temperature of the coffee at time t. (Let y be the temperature of the cup of coffee in degree C, and let t be the time in minutes, with t = 0 corresponding to the time when the temperature was 85 degree C.) dy/dt = -1/50(y-25)

Answer 1

`y(t)=25+Ce^{-(t)/(150)}`

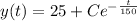
Explanation:

We are given that differential equation

`(dy)/(dt)=-(1)/(50)(y-25)`

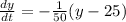
We have to find the expression for the temperature of the coffee at time t.

Let y be the temperature of the coffee in degree C and t be the time in minutes.

At t=0 , y=85 degree Celsius

`(dy)/(y-25)=-(1)/(50)dt`

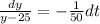
Integrating on both sides

`\int (dy)/(y-25)=-(1)/(50)\int dt`

`ln(y-25)=-(t)/(50)+lnC`

`ln (y-25)-ln C=-(t)/(50)`

`ln(m)-ln (n)=ln(m)/(n)`

`ln(y-25)/(C)=-(t)/(50)`

`(y-25)/(C)=e^{-(t)/(50)}`

`lnx=y\implies x=e^y`

`y-25=Ce^{-(t)/(150)}`

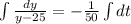
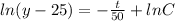
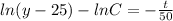
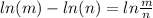
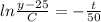
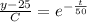
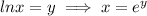
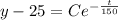
Substitute the value t=0 and y=85 then we get

`85-25=Ce^(0)`

`60=C`

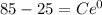
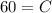
Substitute the value of C

Then , we get

`y-25=60e^{-(t)/(150)}`

`y(t)=25+Ce^{-(t)/(150)}`

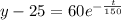
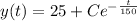
This is required expression for the temperature of the coffee at time t.