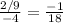Answer:
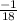
Explanation:
Given that x and y are implicitly as differentiable functions.
xequals=f(t), yequals=g(t),
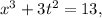
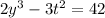
we have to get value of x and y at t =2
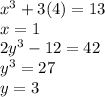
we have to find the slope of the curve at t=2
i.e. we have to find
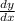
=
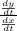 at t=2
at t=2
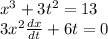
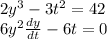
Substitute the values of x and y and also t in these equations to get
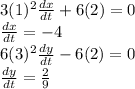
Slope =