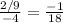Question

Assuming that the equation defines x and y implicitly as differentiable functions xequals=​f(t), yequals=​g(t), find the slope of the curve xequals=​f(t), yequals=​g(t) at the given value of t. x^3+3t^2 =13, 2y^3−3t^2= 42, t=2. The slope of the curve at t=2 is what?

Answer 1

`(-1)/(18)`

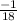
Explanation:

Given that x and y are implicitly as differentiable functions.

xequals=​f(t), yequals=​g(t),

`x^3+3t^2 =13,`

`2y^3-3t^2= 42`

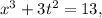
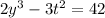
we have to get value of x and y at t =2

`x^3+3(4) = 13\\x =1\\2y^3-12 = 42\\y^3 = 27\\y=3`

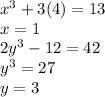
we have to find the slope of the curve at t=2

i.e. we have to find
`(dy)/(dx)`

=
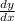
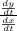`((dy)/(dt) )/((dx)/(dt) )` at t=2

`x^3+3t^2 =13\\3x^2 (dx)/(dt) +6t = 0\\`
`2y^3-3t^2= 42\\6y^2 (dy)/(dt) -6t = 0\\`

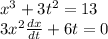
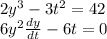
Substitute the values of x and y and also t in these equations to get

`3(1)^2 (dx)/(dt) +6(2) = 0\\(dx)/(dt) =-4\\6(3)^2 (dy)/(dt) -6(2)= 0\\(dy)/(dt)=(2)/(9)`

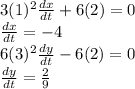
Slope =
`(2/9)/(-4)=(-1)/(18)`