Answer:
We have to change the 'x' value of the point (2, -6) to 3 so the new point is (3, -6).
Explanation:
Given:
The relation is given as:
{(2,4), (-9, 0), (-1, 7), (2, -6)}
The above set is not a function because the 'x' value of 2 has two images or 'y' values.
For
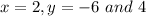
So, this is not a function as for a function each 'x' value should have a unique 'y' value.
In order to make the above relation a function, we need to change the 'x' value of either of the points (2, 4) or (2, -6). Let's change the point (2, -6). We change the value of 'x' such that it doesn't equals any of 'x' values of the given set. So, we can't take 'x' values as 2, -9, and -1. We can take any other value. So, let us take 3 as the value. So, the point becomes (3, -6).
Now, the given relation is a function as each 'x' value has unique 'y' value.
(2, 4), (-9, 0), (-1, 7) and (3, -6)