Question

What are the zeros of the polynomial function f(x)=x^3-5x^2-6x ?

Answer 1

D is the right answer

Explanation:

Answer 2

Option C

The zeros of the polynomial function f(x) = x^3 - 5x^2 - 6x is x = 0 and x = -1 and x = 6

Solution:

Given that polynomial function is f(x) = x^3 - 5x^2 - 6x

We have to find the zeros of polynomial

To find zeros, equate the given polynomial function to 0. i.e f(x) = 0

`x^3 - 5x^2 - 6x = 0`

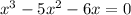
Taking "x" as common term,

`x(x^2 - 5x - 6) = 0`

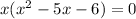
Equating each term to zero, we get

`x=0 \text { and } x^(2)-5 x-6=0`

Thus one of the zeros of function is x = 0

Now let us solve
`x^(2)-5 x-6=0`

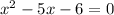
We can rewrite -5x as -6x + x

`x^2 + x - 6x - 6 = 0`

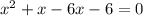
Taking "x" as common from first two terms and -6 as common from next two terms

`x(x + 1) -6(x + 1) = 0`

Taking (x + 1) as common term,

(x + 1)(x - 6) = 0

x + 1 = 0 and x - 6 = 0

x = -1 and x = 6

Thus the zeros of given function is x = 0 and x = -1 and x = 6