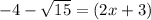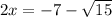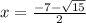Question

What are the solutions of the equation (2x + 3)2 + 8(2x + 3) + 11 = 0? Use u substitution and the quadratic formula to solve

X-

Answer 1

B Edge 2022

Explanation:

Answer 2

`x=(-7+√(15))/(2)`

`x=(-7-√(15))/(2)`

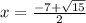
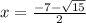
Step-by-step explanation:

we have

`(2x+3)^2+8(2x+3)+1=0`

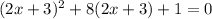
Let

`u=(2x+3)`

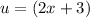
substitute the variable

so

`u^2+8u+1=0`

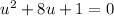
we know that

The formula to solve a quadratic equation of the form

`ax^(2) +bx+c=0`

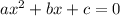
is equal to

`x=\frac{-b(+/-)\sqrt{b^(2)-4ac}} {2a}`

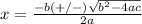
in this problem we have

`u^2+8u+1=0`

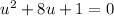
so

`a=1\\b=8\\c=1`

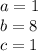
substitute in the formula

`u=\frac{-8(+/-)\sqrt{8^(2)-4(1)(1)}} {2(1)}`

`u=\frac{-8(+/-)√(60)} {2}`

`u=\frac{-8(+/-)2√(15)} {2}`

`u=-4(+/-)√(15)`

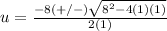
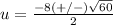
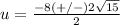
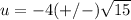
so

`u_1=-4+√(15)`

`u_2=-4-√(15)`

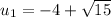
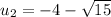
Find the value of x

Remember that

`u=(2x+3)`

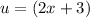
First solution

`-4+√(15)=(2x+3)`

`2x=-4+√(15)-3`

`2x=-7+√(15)`

`x=(-7+√(15))/(2)`

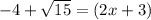
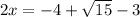
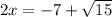
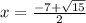
Second solution

`-4-√(15)=(2x+3)`

`2x=-4-√(15)-3`

`2x=-7-√(15)`

`x=(-7-√(15))/(2)`